Number Patterns in the Multiplication Table
A Fun Way to Learn
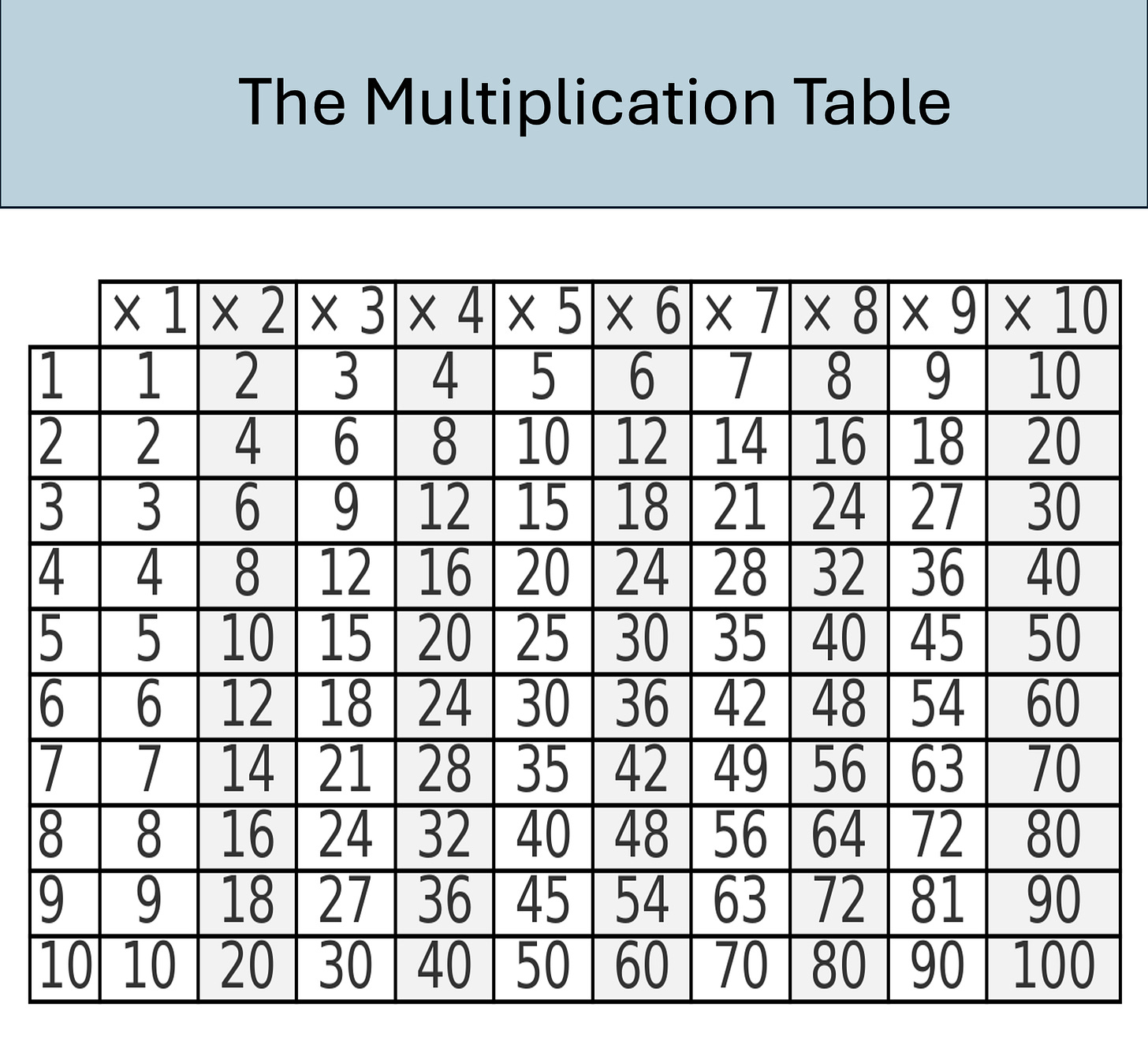
Elementary school students are often taught to memorize the multiplication table by heart, as it serves as the foundation for mastering arithmetic.
The multiplication table is not a collection of random numbers—it contains structured sequences meant to be explored and understood. As children, many of us were simply told to memorize it without being introduced to the number patterns hidden within. Today, I’ll discuss some of these fun patterns, which can make learning more enjoyable and help older students deepen their mathematical understanding and sharpen their pattern recognition skills.
Last-Digit Number Patterns
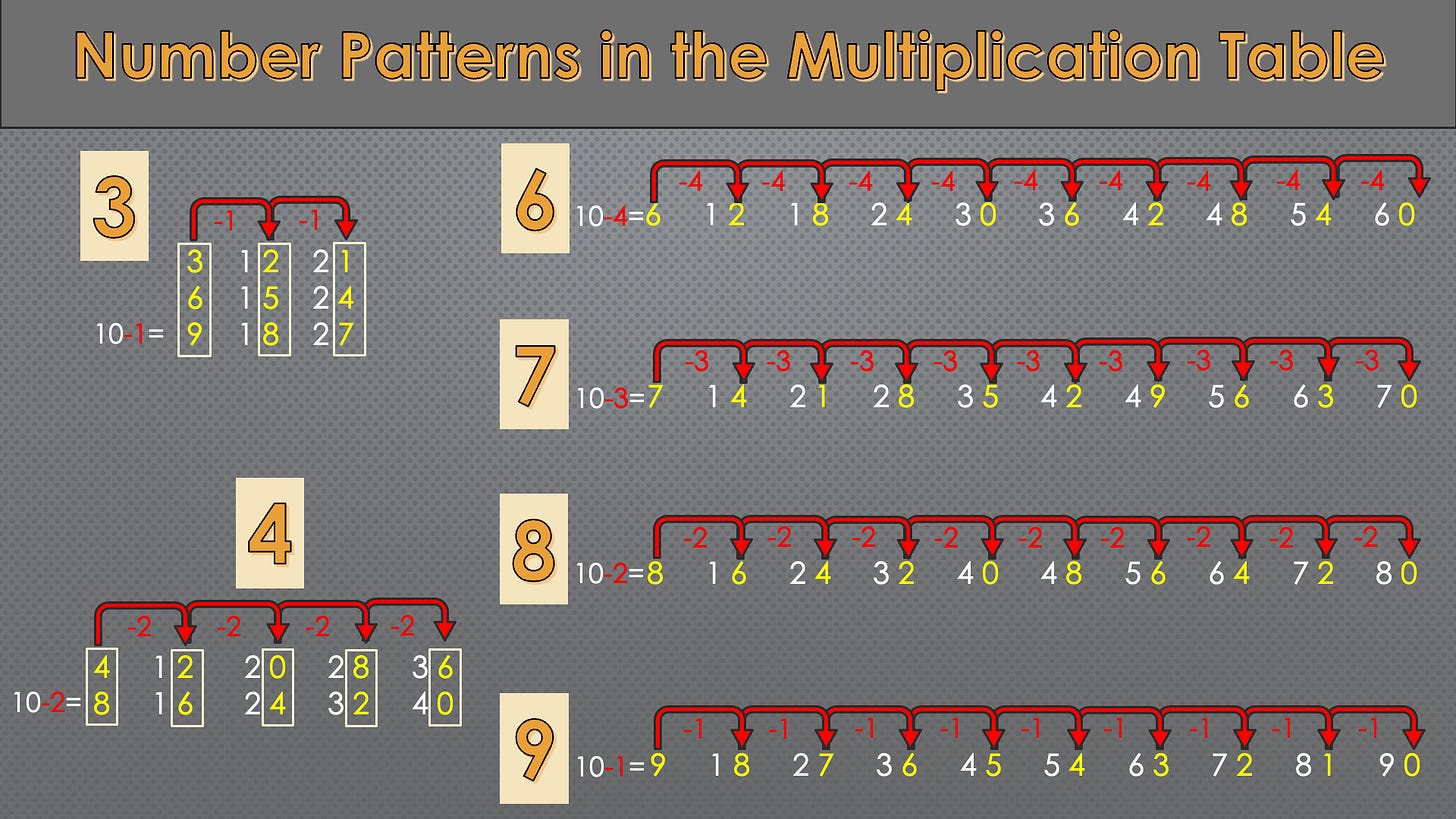
In the table above, every column contains the multiples of a number in successive order. They can be pictured as fence posts sitting at equal distance from each other.
For illustrative purposes, let us study the last digit of the multiples of 3. First, observe that because 10/3 = 3.333, there are three multiples of 3 in the interval 1-10, which are the single-digit numbers
3
6
9
We then ask, what will be the last digit of the next three multiples? The answer is ready to be found from the remainder of 10/3, which is 1. We are now sure the answers are
3-1=2
6-1=5
9-1=8
They correspond to 12, 15, and 18.
The above observation is a direct consequence of our base-10 number system. Essentially, we can imagine ourselves painting one fence post blue out of every three, but at the same time, we are also putting a mark on a post one out of every ten. The two ways of equal-distance counting will consistently differ by the same offset, resulting in the last digit forming a periodic sequence.
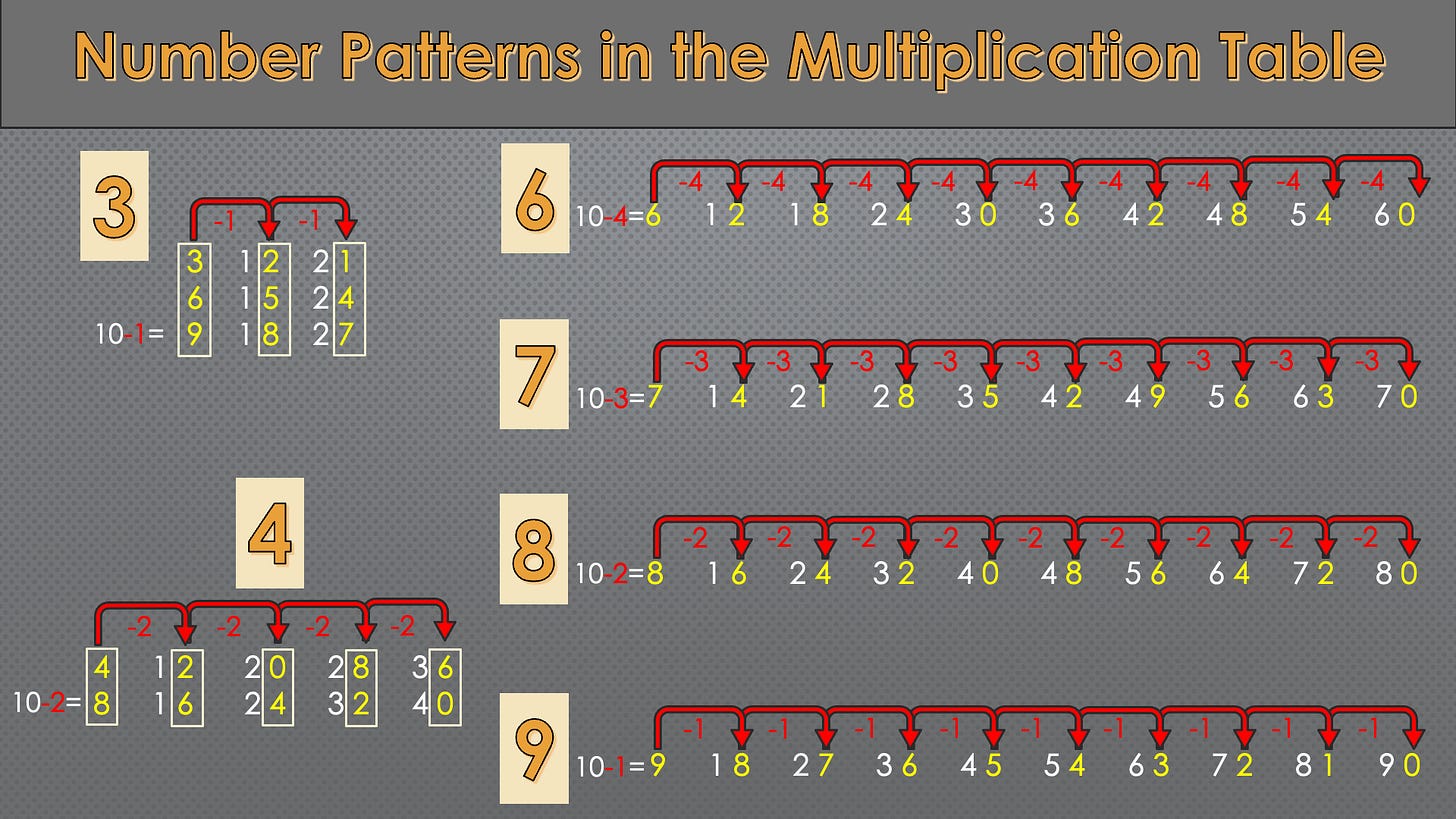
Let me repost the cover picture here, which captures the essence of my explanation above:
Students can understand the pattern by picturing the remainder of, say, 10/3, being “rolled over” to the next interval.
What Do Those Patterns Tell Us?
First, the above patterns are rooted in the interplay between two periodic sequences. In science, such interplay shows up very often, leading to concepts such as phase shifts and interference in physics. When understood as two waves of different frequencies projecting onto each other, the patterns can shed light on some of the most fundamental concepts and phenomena in physics and engineering. Older students can certainly benefit from the rich insights, which can be explored at various levels of complexity.
Second, these patterns provide a method to recreate the multiplication table using primarily simple, single-digit subtractions. Since our brains are way better at processing single-digit arithmetic compared to higher digits, this approach can reinforce children’s memorization of the multiplication table, making the process less prone to mistakes. For older students, these patterns can serve as an algorithmic approach to exploring number properties.
Closing
As I always stressed, pattern recognition is crucial in learning any subject. The observations discussed above can sharpen children’s pattern recognition ability and boost their overall study skills.
Until next time, let math shine your thoughts and build your life.